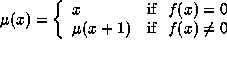We handle partial functions by viewing them as total functions over their domains of convergence. To do so we introduce dom terms, which capture the notion of a domain of convergence. Thus, for a partial function application to be sensible one must prove that the domain of convergence predicate is true for the argument, i.e., that the argument is in the domain of convergence of the function. The introduction of dom terms introduces additional proof obligations into the rules for reasoning about partial functions.
As an example,
the partial function 
producing the smallest root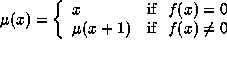 
of f,
has a domain of convergence defined by the predicate
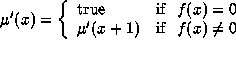as follows.
Thus
is a total function in 
.
In our notation the type of partial
functions from A to B is
A
> B , the application of partial function f to a is
written f[a], recursive functions are expressed as
terms of the form fix(f,x.b), so
function 
of the preceding example is
MU == fix(mu,x. int_eq(f(x); 0; x; mu[x+1])),and
is 
dom(MU) , an elim form
which turns out to have value
\x.rec(mu',x. int_eq(f(x); 0; true; mu(x+1)); MU; x).The domain predicate is derived later; in general, if
A
> B then
\
[x]
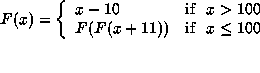
{x :A |dom(f)(x)}->B.
As a second example, the ``91'' function,
has domain
In our notation F and
are
91== fix(F,x. less(100; x; x-10; F[F[x+11]])
\x.rec(F',x.
less(100; x; true; c:F'(x+11)#F'(F[x+11]); 91; x)
Notice that the rec forms defined in the preceding section
must be extended to include the simultaneous definition of the
recursive function.
The new proof rules for these rec terms are only slight
variants of the given rules, so they are not listed here.