Many people have seen formal proofs only during courses
in logic. Most such courses begin with rules in which
the propositional connectives 
and 
correspond to
the natural language connectives ``and'',``or'',``not'' and ``implies'',
respectively. If the nature of propositions is left
unanalyzed except for their propositional structure, and if
the unanalyzed parts are denoted by variables such as P, Q and R,
then the resulting forms are called
propositional formulas.
For example,
is an instance of a propositional formula.
Let us take a propositional formula which we recognize to be true and
analyze why we believe it. We will then
translate the argument into Nuprl
. Consider
the formula
.
We argue for its truth in the following fashion.
If we assume
then we
need to show
.
Supposing
is also
true, we need to show
;
that is, we must
show that P is true if Q is. Therefore assume Q is true.
Now we know
,
so we can consider two cases;
if we establish the truth of P in each case then we have
finished the proof.
In the first case, where P is true, we are done immediately.
If 
is true, then because
holds we know that 
is true, for
that is the meaning of
implication.
Therefore, both Q and 
follow from our assumptions.
This, of course, is a contradiction, and since
from a contradiction we can derive anything,
P again is true.
This finishes the argument.
To formalize this argument we use the definitions
given in chapter 3 of the constructive propositional connectives
and of all.
We also recognize that to say P and
Q are arbitrary propositions can be taken to mean that they are
arbitrary members of the universe 
.
A reasonable formalization of the assertion to be proved, then,
is
all P:U1. all Q:U1. (P|~P) => (~P=>~Q) => (Q=>P).
Following are a few snapshots from a session in which this theorem is proved. Note the similarity between the steps of the formal proof and the steps of the informal proof given above. In the first two windows below, we see the use of the intro rule as the formal analogue of the ``assume'' or ``suppose'' of the informal argument.
,--------------------------------------, |EDIT THM prop1 | |--------------------------------------| |# top 1 | |1. P:(U1) | |>> (all Q:U1. | | (P|~P)=>(~P=>~Q)=>(Q=>P)) | | | |BY intro at U2 | | | |1# 1. P:(U1) | | 2. Q:(U1) | | >> ( (P|~P)=>(~P=>~Q)=>(Q=>P) ) | | | |2* 1. P:(U1) | | >> (U1) in U2 | '--------------------------------------'
,--------------------------------------, |EDIT THM prop1 | |--------------------------------------| |# top 1 1 1 | |1. P:(U1) | |2. Q:(U1) | |3. (P|~P) | |>> (~P=>~Q)=>(Q=>P) | | | |BY intro at U1 | | | |1# 1. P:(U1) | | 2. Q:(U1) | | 3. (P|~P) | | 4. (~P=>~Q) | | >> (Q=>P) | | | |2* 1. P:(U1) | | 2. Q:(U1) | | 3. (P|~P) | | >> (~P=>~Q) in U1 | '--------------------------------------'
In the main goal of the next window is the result of five consecutive intros. The step shown below uses elim to do the case analysis of the informal argument.
,----------------------------------------------, |EDIT THM prop1 | |----------------------------------------------| |# top 1 1 1 1 1 | |1. P:(U1) | |2. Q:(U1) | |3. (P|~P) | |4. (~P=>~Q) | |5. Q | |>> P | | | |BY elim 3 | | | |1* 1. P:(U1) | | 2. Q:(U1) | | 3. (P|~P) | | 4. (~P=>~Q) | | 5. Q | | 6. P | | >> P | | | |2# 1. P:(U1) | | 2. Q:(U1) | | 3. (P|~P) | | 4. (~P=>~Q) | | 5. Q | | 6. ~P | | >> P | '----------------------------------------------'
In the main goal of the next window we see that the conclusion follows from hypotheses 4, 5 and 6. To use hypothesis 4 we elim it.
,---------------------------,--------------------------, |EDIT THM prop1 |EDIT rule of prop1 | |---------------------------|--------------------------| |# top 1 1 1 1 1 2 |elim 4 | |1. P:(U1) | | |2. Q:(U1) | | |3. (P|~P) | | |4. (~P=>~Q) | | |5. Q | | |6. ~P | | |>> P '--------------------------' | | |BY <refinement rule> | '-----------------------------------------------'
Nuprl will then require us to prove P, which is trivial since it is a hypothesis, and then to prove P given the new hypothesis Q, which is also trivial, since we will have two contradictory hypotheses. The auto--tactic will handle both of these subgoals. This completes the proof.
The preceding proof gave a few examples of
the application of intro and elim rules to propositional
formulas. A more complete account is given in figure
, which shows a set of rules for the
constructive propositional
calculus in a format suitable to a refinement logic, with the
premises (subgoals) below the conclusion (goal).
If a goal has the form of one of the goals
in the table, then specifying
intro or elim
as the Nuprl
rule will generate
the subgoals shown
with the exception that => intro will have a
second subgoal, P in U1, which will usually be proved
by the auto--tactic.
The hypotheses shown in the
goals of the elim rules will in general be
surrounded by other hypotheses, and in
all of the rules the entire hypothesis list is copied to the
subgoals with any new hypotheses added to the end.
Recall that P is really P => false, so rules
dealing with negation can be derived from the given rules.
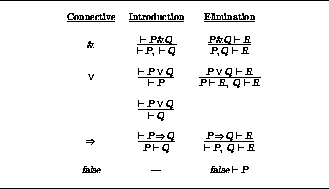
Figure: Refinement Rules for the Constructive Propositional Logic